“Begin to write down solving reports for problems on LeetCode Algorithm problems-set….”
LeetCode题解 - Regular Expression Matching
题目难度: Hard
题目地址: No.10 Regular Expression Matching
题目描述:
Given an input string (s) and a pattern (p), implement regular expression matching with support for '.' and '*'.
'.' Matches any single character.
'*' Matches zero or more of the preceding element.
The matching should cover the entire input string (not partial).
Note:
s could be empty and contains only lowercase letters a-z.
p could be empty and contains only lowercase letters a-z, and characters like . or *.
给定两个输入字符串,首个字符串s为须检测串,第二个字符串为模板字符串p,其可由小写字符,以及符号.和*组成。
.可表示任何一个小写字符
*可表示为0个或多个其之前的符号组成的字符串
.*为特殊情况,可以表示从空字符串到任意长度的任何字符组成的字符串
字符串s,p都可以是空串,其中s只包含小写字符
请你根据以上的正则表达式匹配规则,判断输入串s是否能够匹配模板串p,根据结果输出true or false
题目思路:
- 本题目的总体难度并不高,无非是一般情况下字符串正则匹配的缩减版,对于一般的小写字符以及
.我们都能轻易地判断是否符合,然而对于’*‘则需要通过检查前一位字符进行0到多位的字符串拓展匹配原串。 - 关于匹配规则以及实现方法我们可以分为以下两类,第一种是直观的迭代匹配法,思想简单复杂度高,但却是最容易实现的写法;第二种是动态规划DP写法,采用dp数组存储匹配生成串,是空间换时间的写法。
题目解法:
-
迭代法
-
解法概要
迭代求解字符串匹配问题,首先需要检测空字符串情况,其次在该步迭代中对第一位字符非
*情况进行是否成功匹配判断,以及后一位是否为*进行不同的迭代操作,综合各项匹配Flag判断迭代返回值。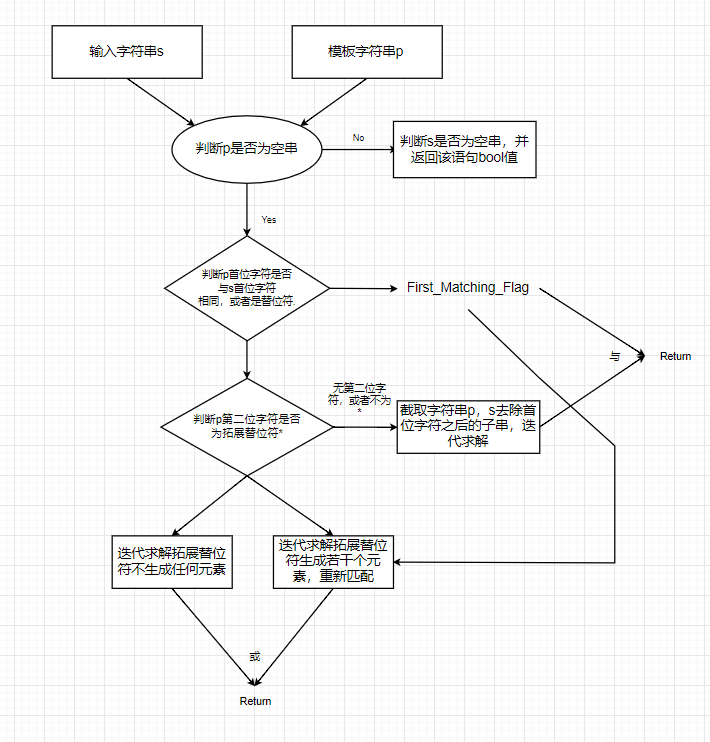
-
C++代码
class Solution { public: bool isMatch(string s, string p) { // Use recursive method if(p.empty()) return s.empty(); bool match_flag = (p[0] == s[0] || p[0] == '.') && !(s.empty()); // Judge and make recursion if(p.size() >= 2 && p[1] == '*') { bool zero_star_flag = isMatch(s, p.substr(2)); bool have_star_flag = match_flag && isMatch(s.substr(1), p); return zero_star_flag || have_star_flag; }else { return match_flag && isMatch(s.substr(1), p.substr(1)); } } }; -
运行结果

可以看到,普通的迭代法求解十分耗时,并且不断地遍历根据规则生成的字符串的各种情况,时间复杂度很高,于是我们需要引入接下来的动态规划解法。
-
动态规划法
-
解法概要
开辟
s.len X p.len大小的二维数组dp,我们定义以下操作:- dp[i][j] = dp[i-1][j-1], 当且仅当p[j-1] != ‘*’, 同时对应位置的字符匹配成功,即(p[j-1] == ‘.’ or s[i-1] == p[j-1])。
- dp[i][j] = dp[i][j-2], 当且仅当p[j-1] == ‘*’, 并且该替位符重复了0次。
- dp[i][j] = dp[i-1][j], 当且仅当p[j-1] == ‘*’, 并且重复了若干次,即(s[i-1] == p[j-2] or p[j-2] == ‘.’)
-
C++代码
class Solution { public: bool isMatch(string s, string p) { int m = s.length(), n = p.length(); // Initialize the dp vector<vector<bool> > dp(m + 1, vector<bool> (n + 1, false)); dp[0][0] = true; for (int i = 0; i <= m; i++) for (int j = 1; j <= n; j++){ if(p[j-1] != '*') { if(i > 0 && (s[i - 1] == p[j - 1] || p[j - 1] == '.')) dp[i][j] = dp[i-1][j-1]; else dp[i][j] = false; }else { if(i > 0 && (s[i - 1] == p[j - 2] || p[j - 2] == '.') dp[i][j] = dp[i-1][j]; else dp[i][j] = dp[i][j-2]; } } return dp[m][n]; } };
-
运行结果
